Kvantitativa forskningsprocessen & beskrivande statistik
Enes Al Weswasi
Kriminologiska institutionen, Stockholms universitet
deskriptiv-statistik.netlify.app
Översikt
1. Kvantitativa forskningsprocessen
2. Datanivåer och variabeltyper
3. Univariat beskrivande statistik
4. Grafisk resultatpresentation
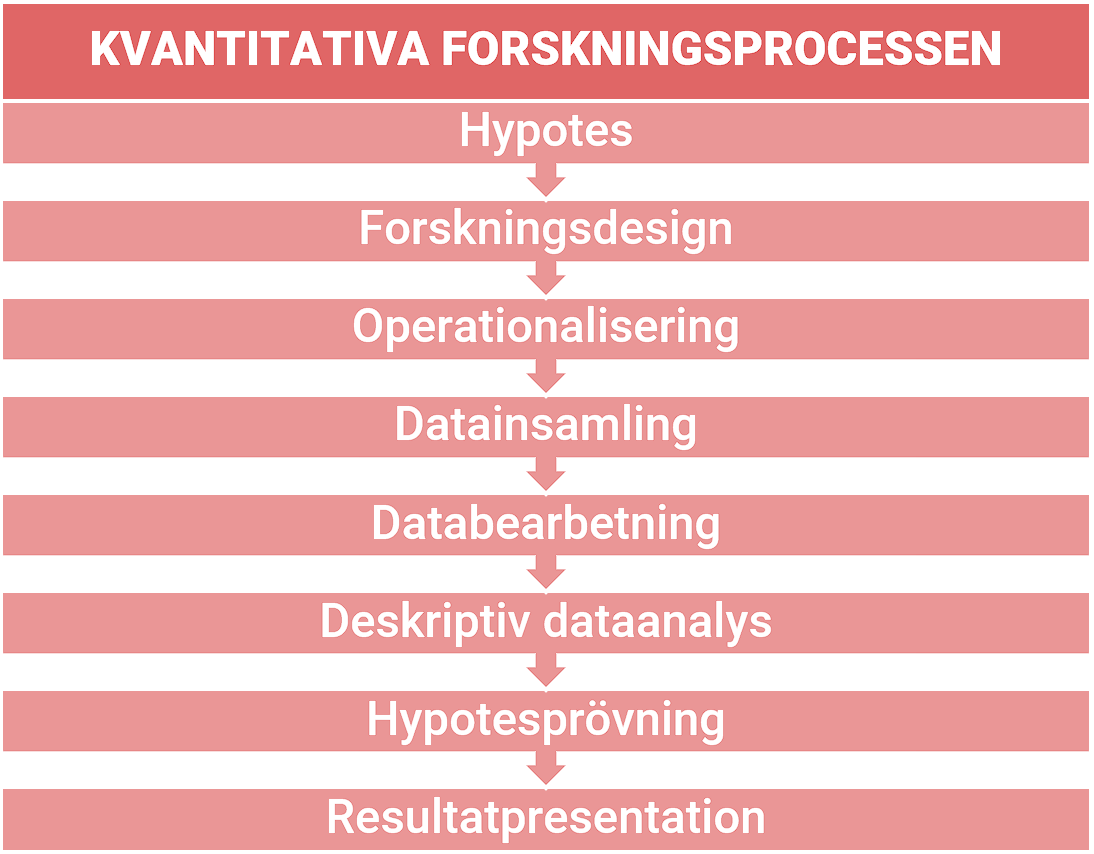
Kvantitativa forskningsprocessen
Kvantitativa forskningsprocessen
Kvantitativa metod är ett samlingsbegrepp metoder för insamling av siffermässig data eller kvantifiering av data till siffror. Statistiska beräkningar används som bearbetningsmetoder.
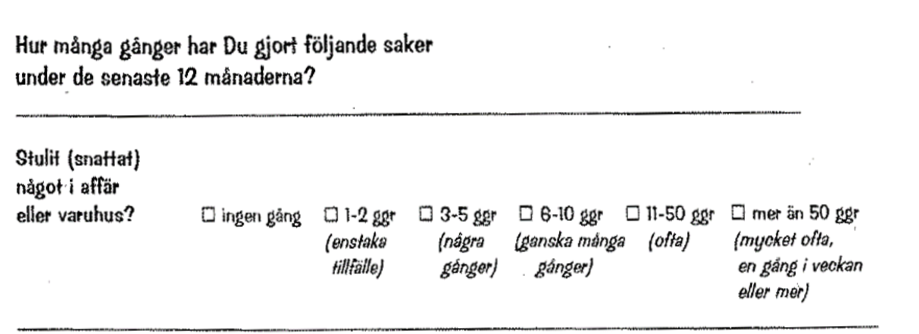
Operationalisering
Att göra ett begrepp som vi ämnar att studera mätbart för att på så sätt kunna lagra informationen i form av variabler. Grunden till empirisk forskning. Att göra ett begrepp mätbara kräver att vi först tydligt definier begreppet.
Vad betyder brottslighet och hur mäter vi brottslighet?
Vad betyder självkontroll och hur mäter vi självkontroll?

Operationalisering
Operationalisering

Variabel
Defineras som ett fenomen vars värde kan variera från observation till observation. Motsatsen till en variabel är en konstant.
Analysenhet är den eller de enheter som du analyserar i din studie
| Person ID | Ålder |
|---|---|
| 1 | 26 |
| 2 | 24 |
| 3 | 25 |
| 4 | 24 |
| 5 | 24 |
| 6 | 26 |
Variabel
Defineras som ett fenomen vars värde kan variera från observation till observation. Motsatsen till en variabel är en konstant.
Analysenhet är den eller de enheter som du analyserar i din studie
| Land | Intagna (per 100 000) |
|---|---|
| Sverige | 235 |
| Danmark | 249 |
| Norge | 208 |
| Finland | 138 |
| Island | 164 |
Variabel
Defineras som ett fenomen vars värde kan variera från observation till observation. Motsatsen till en variabel är en konstant.
Analysenhet är den eller de enheter som du analyserar i din studie
| År | Återfall (%) |
|---|---|
| 2013 | 40 |
| 2014 | 40 |
| 2015 | 39 |
| 2016 | 39 |
| 2017 | 39 |
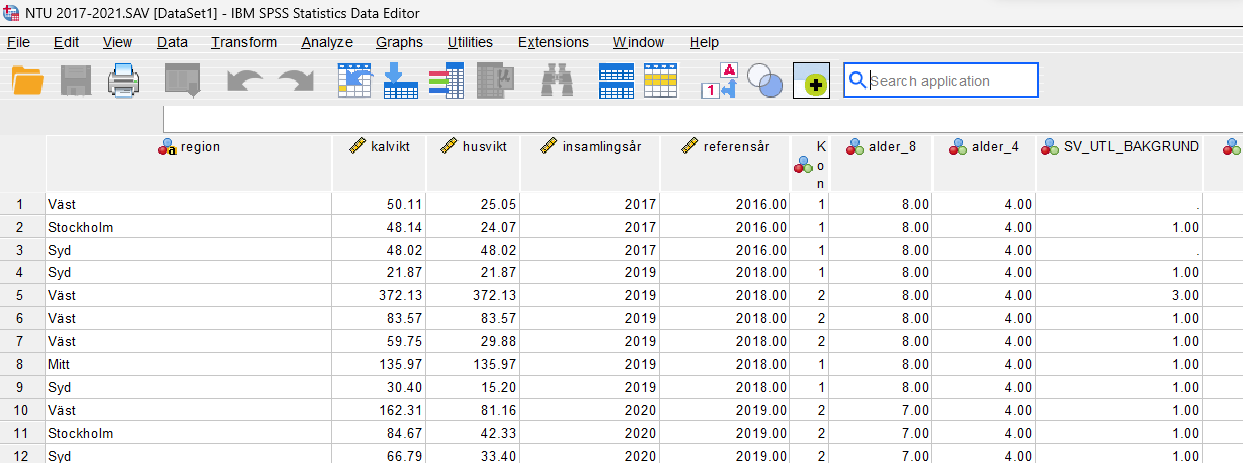
Dataset
- En samling data (eller variabler) som behandlas tillsammans för ett bestämt ändamål i ett datorprogram.
Dataset
En samling data (eller variabler) som behandlas tillsammans för ett bestämt ändamål i ett datorprogram.
Data som numerisk information (även om informationen uttrycks i bokstäver).
Dataset
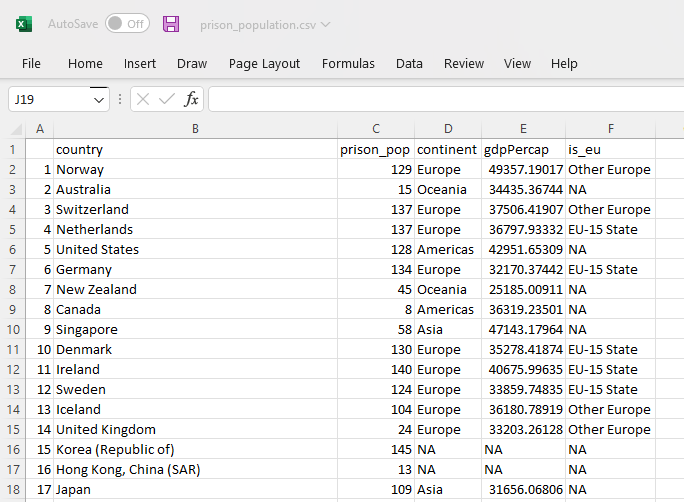
Dataset
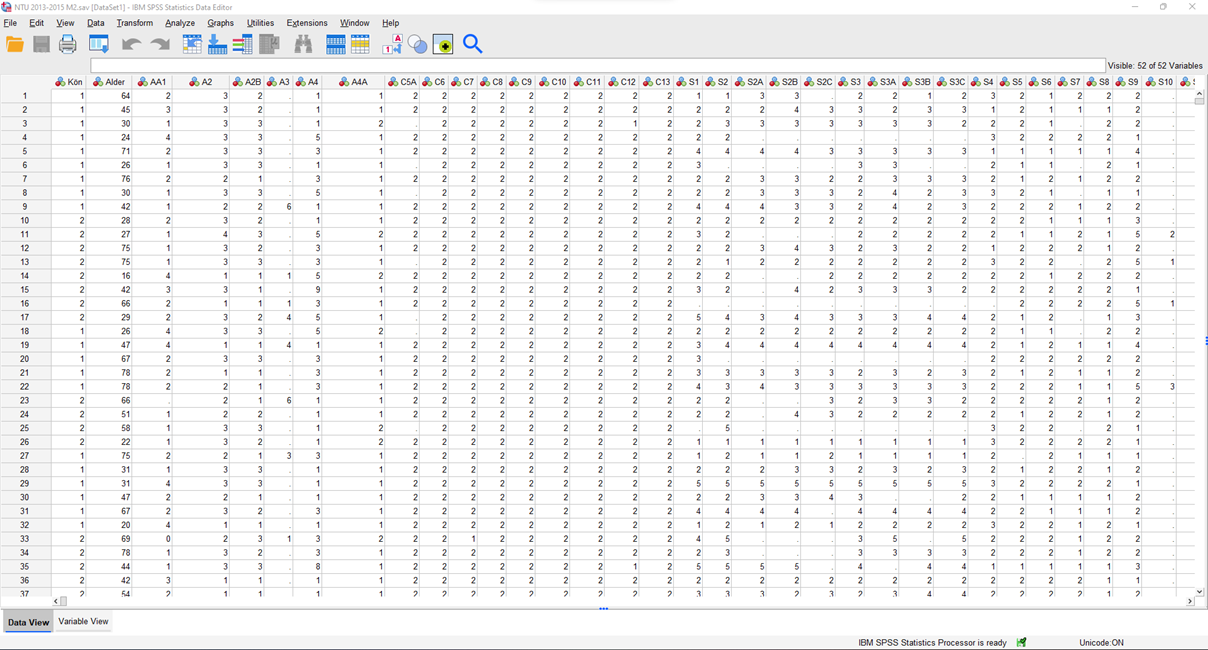
Dataset

Variabeltyper och datanivåer
Datanivå
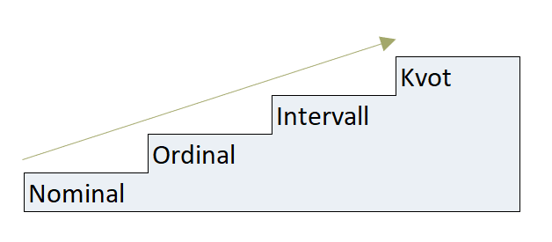
- Variablernas matematiska karaktär.
- På lägre nivåer har siffrorna betydelser som är egentiligen bara etiketter.
- På högsta mätnivåer har siffrorna numeriska betydelser och kan anlyseras på en mängd olika sätt.
- Det är viktigt att veta vilken typ av variabel som du använder, så att du kan välja rätt statistiska test, centralmått, spridningsmått och grafisk presentation.
Fiktivt dataset
| Person ID | Brottstyp | Ålder | Kön | Civiltillstånd | SES |
|---|---|---|---|---|---|
| 1 | Inbrott | 30 | Man | Gift | Medelklass |
| 2 | Misshandel | 31 | Kvinna | Ogift | Arbetarklass |
| 3 | Misshandel | 28 | Man | Ogift | Underklass |
| 4 | Snatteri | 29 | Man | Ogift | Arbetarklass |
| 5 | Snatteri | 31 | Man | Gift | Arbetarklass |
| 6 | Annat | 29 | Kvinna | Gift | Överklass |
| 7 | Annat | 29 | Kvinna | Gift | Medelklass |
| 8 | Misshandel | 32 | Man | Ogift | Arbetarklass |
| 9 | Snatteri | 30 | Man | Ogift | Medelklass |
| 10 | Annat | 31 | Man | Ogift | Underklass |
| 11 | Annat | 31 | Kvinna | Gift | Arbetarklass |
Nominal
Icke-numeriska kategorier som representerar något annat än siffror.
Kategorierna kan ej rangordnas.
| Person ID | Kön |
|---|---|
| 1 | Man |
| 2 | Kvinna |
| 3 | Man |
| 4 | Man |
| 5 | Man |
| 6 | Kvinna |
| 7 | Kvinna |
| 8 | Man |
| 9 | Man |
| 10 | Man |
| 11 | Kvinna |
Nominal
Icke-numeriska kategorier som representerar något annat än siffror.
Kategorierna kan ej rangordnas.
Kan tilldelas ett numeriskt värde för statistiska ändamål.
Det förekommer tillfällen då dessa värden är sorterade. Detta betyder dock ej att siffrorna kan användas för matematiska beräkningar.
| Person ID | Man |
|---|---|
| 1 | 1 |
| 2 | 0 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 0 |
| 7 | 0 |
| 8 | 1 |
| 9 | 1 |
| 10 | 1 |
| 11 | 0 |
Nominalvariabler i datasetet
| Person ID | Brottstyp | Ålder | Kön | Civiltillstånd | SES |
|---|---|---|---|---|---|
| 1 | Inbrott | 30 | Man | Gift | Medelklass |
| 2 | Misshandel | 31 | Kvinna | Ogift | Arbetarklass |
| 3 | Misshandel | 28 | Man | Ogift | Underklass |
| 4 | Snatteri | 29 | Man | Ogift | Arbetarklass |
| 5 | Snatteri | 31 | Man | Gift | Arbetarklass |
| 6 | Annat | 29 | Kvinna | Gift | Överklass |
| 7 | Annat | 29 | Kvinna | Gift | Medelklass |
| 8 | Misshandel | 32 | Man | Ogift | Arbetarklass |
| 9 | Snatteri | 30 | Man | Ogift | Medelklass |
| 10 | Annat | 31 | Man | Ogift | Underklass |
| 11 | Annat | 31 | Kvinna | Gift | Arbetarklass |
Ordinal
Kategorier kan rangordnas från hög till låg, mer eller mindre
Värdet har bara betydelse i förhållande till andra värden
Kan inte summera eller subtrahera dessa värden

Ordinal
Kategorier kan rangordnas från hög till låg, mer eller mindre
Värdet har bara betydelse i förhållande till andra värden
Kan inte summera eller subtrahera dessa värden
| Person ID | SES |
|---|---|
| 1 | Medelklass |
| 2 | Arbetarklass |
| 3 | Underklass |
| 4 | Arbetarklass |
| 5 | Arbetarklass |
| 6 | Överklass |
| 7 | Medelklass |
| 8 | Arbetarklass |
| 9 | Medelklass |
| 10 | Underklass |
| 11 | Arbetarklass |
Intervall
Ekvidistans - lika avstånd mellan värdena.
Med dessa variabler kan man utföra alla tänkbara matematiska beräkningar.

Kvot
Ekvidistans - lika avstånd mellan värdena.
Med dessa variabler kan man utföra alla tänkbara matematiska beräkningar.
Har en absolut/meningsfull nollpunkt.
| Person ID | Ålder |
|---|---|
| 1 | 30 |
| 2 | 31 |
| 3 | 28 |
| 4 | 29 |
| 5 | 31 |
| 6 | 29 |
| 7 | 29 |
| 8 | 32 |
| 9 | 30 |
| 10 | 31 |
| 11 | 31 |
Två olika typer av intervall/kvot-variabler
Diskret variabel - grundläggande måttenhet som inte kan delas.
Två olika typer av intervall/kvot-variabler
Diskret variabel - grundläggande måttenhet som inte kan delas.
Antal brottmålsdomar
Befolkning
Antal syskon
Antal skilsmässor
Två olika typer av intervall/kvot-variabler
Diskret variabel - grundläggande måttenhet som inte kan delas.
Antal brottmålsdomar
Befolkning
Antal syskon
Antal skilsmässor
Kontinuerlig variabel - kan i teorin vara oändligt delbar.
Två olika typer av intervall/kvot-variabler
Diskret variabel - grundläggande måttenhet som inte kan delas.
Antal brottmålsdomar
Befolkning
Antal syskon
Antal skilsmässor
Kontinuerlig variabel - kan i teorin vara oändligt delbar.
Ålder
Tid i fängelse
Datanivåer

Antal anmälda brott under en månad på SU.
Vilken datanivå?
Beskrivande statistik
Beskrivande statistik
Två typer av statistik:
Beskrivande statistik är en gren inom statistiken som går ut på att beskriva och sammanfatta en samling data eller variabler. Data kan till exempel beskrivas med hjälp av centralmått och spridningsmått.
Den beskrivande statistiken skiljer sig från inferentiell statistik, som går ut på att dra generella slutsatser om en population med hjälp av stickprov.
Beskrivande statistik
Univariat - sammanfattar eller beskriver fördelningen av en variabel
Beskrivande statistik
Univariat - sammanfattar eller beskriver fördelningen av en variabel
Bivariat - beskriver förhållandet mellan två variabler
Beskrivande statistik
Univariat - sammanfattar eller beskriver fördelningen av en variabel
Bivariat - beskriver förhållandet mellan två variabler
Multivariat - beskriver förhållandet mellan tre eller flera variabler
Univariat beskrivande statistik
Sammanfatta information om enstaka variabler.
Presentera resultat på ett lättförståeligt sätt.
Information såsom dess mittpunkt (centralmått) och dess spridning (spridningsmått).
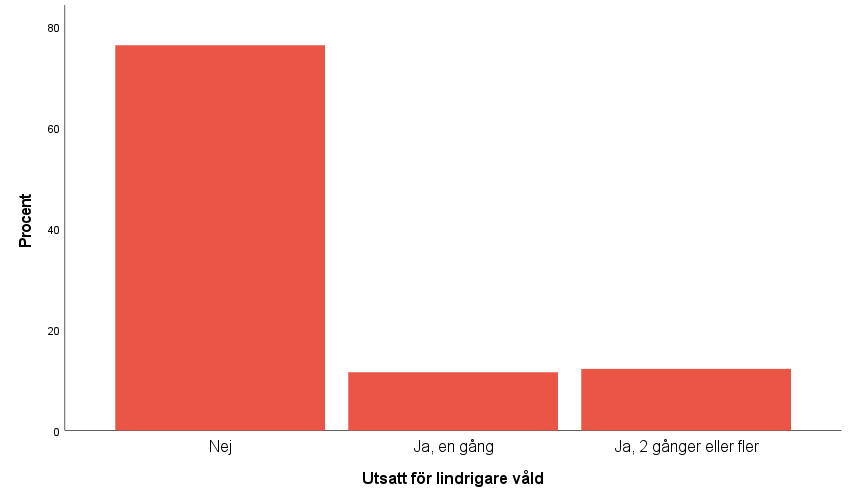
Absolut frekvens
Antal förekomster av enskilda variabelvärden.
## Brottstyp n## 1 Annat 4## 2 Inbrott 1## 3 Misshandel 3## 4 Snatteri 3| Person ID | Brottstyp |
|---|---|
| 1 | Inbrott |
| 2 | Misshandel |
| 3 | Misshandel |
| 4 | Snatteri |
| 5 | Snatteri |
| 6 | Annat |
| 7 | Annat |
| 8 | Misshandel |
| 9 | Snatteri |
| 10 | Annat |
| 11 | Annat |
Absolut frekvens
Problematiska vid numeriska variabler.
Absolut frekvens
| Person ID | Ålder |
|---|---|
| 1 | 19 |
| 2 | 30 |
| 3 | 29 |
| 4 | 24 |
| 5 | 30 |
| 6 | 31 |
| 7 | 32 |
| 8 | 29 |
| 9 | 29 |
| 10 | 31 |
| 11 | 28 |
## Ålder n## 1 14 1## 2 15 1## 3 16 1## 4 17 3## 5 18 5## 6 19 19## 7 20 16## 8 21 26## 9 22 32## 10 23 41## 11 24 61## 12 25 68## 13 26 82## 14 27 92## 15 28 98## 16 29 90## 17 30 85## 18 31 76## 19 32 61## 20 33 42## 21 34 37## 22 35 25## 23 36 17## 24 37 10## 25 38 4## 26 39 2## 27 40 1## 28 41 3## 29 45 1Absolut frekvens
Intervall- och kvotvariablervariabler kan kodas om till ordinala variabler.
Vi offrar vissa detaljer för att få en tydligare tabell.
Exempelvis till åldersspann:
Åldersspann 0-15 år gammal
Åldersspann 16-25 år gammal
Åldersspann 26-40 år gammal
Åldersspann >40 år gammal
Absolut frekvens
| Person ID | Ålder_kategorier |
|---|---|
| 1 | 16-25 |
| 2 | 26-40 |
| 3 | 26-40 |
| 4 | 16-25 |
| 5 | 26-40 |
| 6 | 26-40 |
| 7 | 26-40 |
| 8 | 26-40 |
| 9 | 26-40 |
| 10 | 26-40 |
## Ålder_kategorier n## 1 0-15 2## 2 16-25 272## 3 26-40 722## 4 >40 4Absolut frekvens
Av 1 846 personer med elektronisk fotboja så återföll 746 i brott.
Svårt att intuitivt förstå förhållandet mellan de som återföll och de som ej återföll.
Andel (också kallad relativ frekvens)
Lättare om man beskriver det som:
- Andel av personer med fotboja som återföll i brott var 0.4.
Andel (också kallad relativ frekvens)
a = andel
f = frekvens/antal fall i någon kategori
N = antalet fall i alla kategorier
a=fN
Andel (också kallad relativ frekvens)
Av 1 846 personer med elektronisk fotboja så återföll 746 i brott.
a = 746 / 1 846
a = 0.4041
Andel av personer med fotboja som återföll i brott var 0.4.
a=fN
Andel i procent
Effektivaste sättet att beskriva förhållanden är:
~40 procent av personer med fotboja återföll i brott.
Andel i procent
p = procent
f = frekvens/antal fall i någon kategori
N = antalet fall i alla kategorier
p=fN∗100
Andel i procent
Av 1 846 personer med elektronisk fotboja återföll 746 i brott.
p = (746 / 1 846) x 100
p = 0.4041 x 100
p = 40.41
~40 procent av personer med fotboja återföll i brott.
p=fN∗100
Frekvensfördelning , andel och procent i tabell
| Frekvenser | Andel | Procent | Kummulativ procent | |
|---|---|---|---|---|
| Snatteri | 585 | 0.39 | 39 | 39 |
| Annat | 465 | 0.31 | 31 | 70 |
| Inbrott | 313 | 0.21 | 20.87 | 90.87 |
| Misshandel | 137 | 0.09 | 9.13 | 100 |
| Total | 1500 | 1 | 100 | 100 |
Beskrivande statistik: Centralmått
Centralmått
Tre typer av centralmått:
Typvärde
Median
Medelvärde
Används för att beskriva urvalets tyngdpunkt.
Ditt val av centralmått beror på datanivån för variabel som du analyserar.
Typvärde
Det värde som förekommer flest gånger.
Typvärde kan användas för variabler på alla datanivåer.
Det är dock det enda centralmåttet som går att använda för nominala variabler.
Exempel: Vilket är typvärdet i följande urval?
- 70, 82, 90, 98, 82
Typvärde
Det värde som förekommer flest gånger.
Typvärde kan användas för variabler på alla datanivåer.
Det är dock det enda centralmåttet som går att använda för nominala variabler.
Exempel: Vilket är typvärdet i följande urval?
- 70, 82, 90, 98, 82
Typvärde
Vilket värde är vårt typvärde i brottsdatasetet?
| Frekvenser | |
|---|---|
| Snatteri | 585 |
| Annat | 465 |
| Inbrott | 313 |
| Misshandel | 137 |
| Total | 1500 |
Median
Den exakta mitten av en fördelning av värden.
Hälften av urvalet hamnar över medianen, den andra hälften under.
För att hitta medianen så måste du först rangordna värdena från lägst till högst.
Användas för intervall- och kvotvariabler men framförallt ordinala variabler.
| Person id | Antal brottsmisstankar |
|---|---|
| 1 | 21 |
| 2 | 14 |
| 3 | 11 |
| 4 | 17 |
| 5 | 16 |
| 6 | 19 |
| 7 | 16 |
| 8 | 14 |
| 9 | 15 |
Medelvärde
Det mest använda centralmåttet.
Används för intervall- och kvotvariabler.
Kan användas för ordinala skalor men med försiktighet vid.
Exempel:
Genomsnittliga resultatet på ett prov
Genomsnittliga antalet barn per kvinna
Genomsnittliga längden på ett fängelsestraff
Medelvärde
Medelvärdet representeras vanligen av symbolen (på svenska ”x-tak”, på engelska ”x-bar”).
Kan också uttryckas med bokstaven m.
För att räkna ut medelvärdet summerar du alla värden och dividerar därefter med antalet värden.
¯¯¯x
Medelvärde
Genomsnittlig våldsutsatthet under ett år:
2, 3, 4, 6, 6, 6, 8, 9, 10, 11, 14, 16, 18
¯¯¯x=(2+3+4+⋯+14+16+18)/13
¯¯¯x=112/13
¯¯¯x=8,6
Genomsnittligt våldsutsatthet är 8,6.
¯¯¯x=∑xN
Centralmått
Med undantag för nominala variabler så är det upp till dig att bestämma vilket centralmått som fungerar bäst.
Till stor del så beror detta på vilken fråga du försöker besvara.
Kom ihåg att ditt val kommer att få konsekvenser.
Dina egna fördomar och åsikter kan påverka ditt val av mått.

Vilket centralmått spelar roll
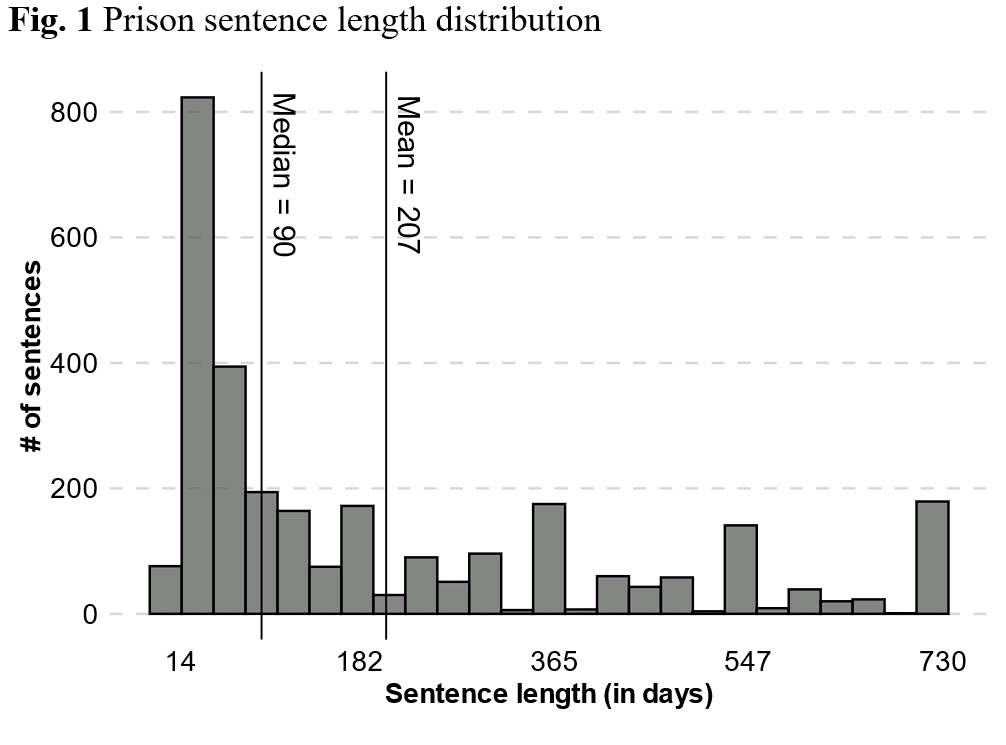
Vilket centralmått spelar roll - Ungdomsbrottslighet?
Åldersfördelning bland 25 intagna.
55 19 18 16 19 16 15 18 20 20 19 16 23 15 17 16 20 55 18 65 16 18 17 19 18
Typvärde = 16
Median = 18
Medelvärde = 23
Vilket centralmått spelar roll - Ungdomsbrottslighet?
Åldersfördelning bland 25 intagna.
55 19 18 16 19 16 15 18 20 20 19 16 23 15 17 16 20 55 18 65 16 18 17 19 18
Typvärde = 16
Median = 18
Medelvärde = 23
Grafisk resultatpresentation
Stapeldiagram
Används främst för kategoriska variabler
## Brottstyp n## 1 Annat 437## 2 Inbrott 253## 3 Misshandel 174## 4 Snatteri 636Stapeldiagram
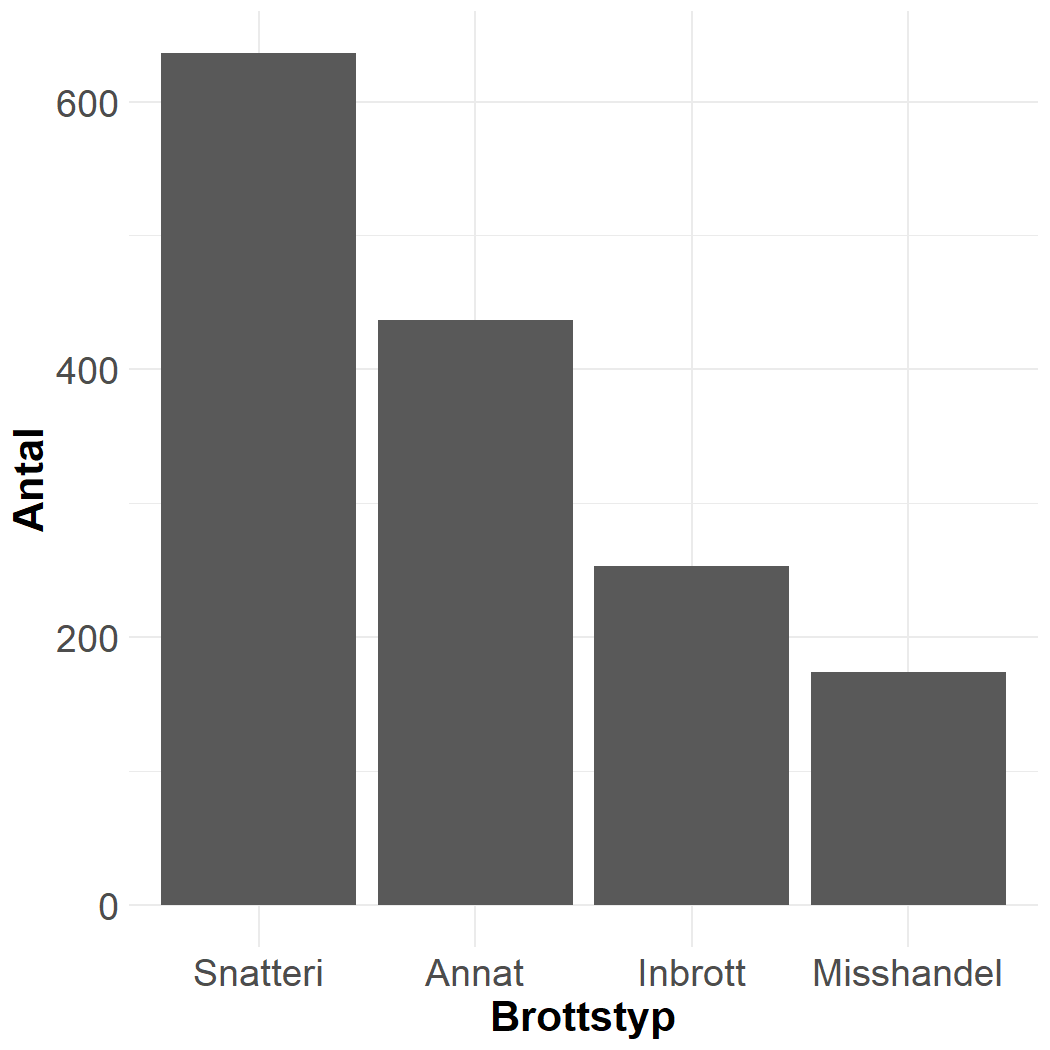
Stapeldiagram
Stapeldiagram
Histogram
Används främst för numeriska variabler.
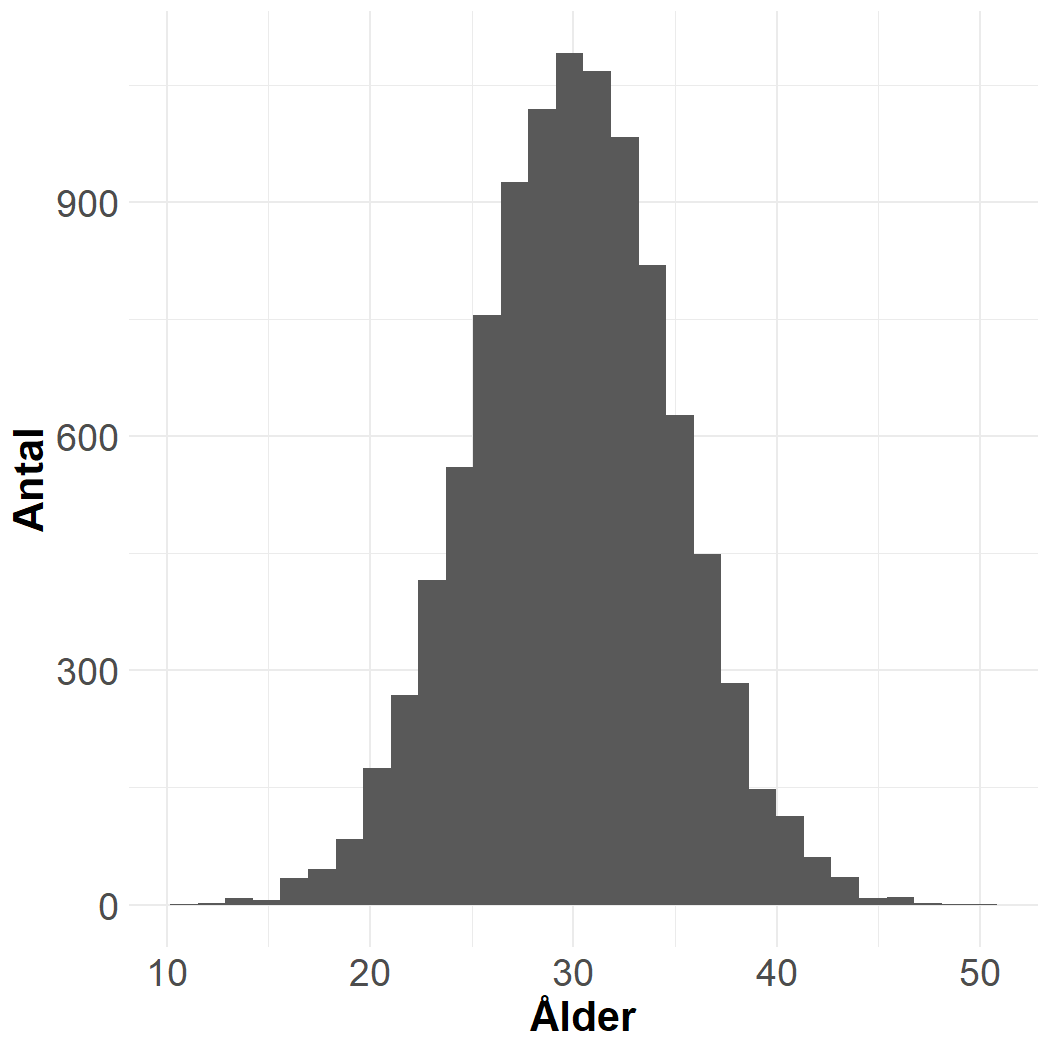
Histogram
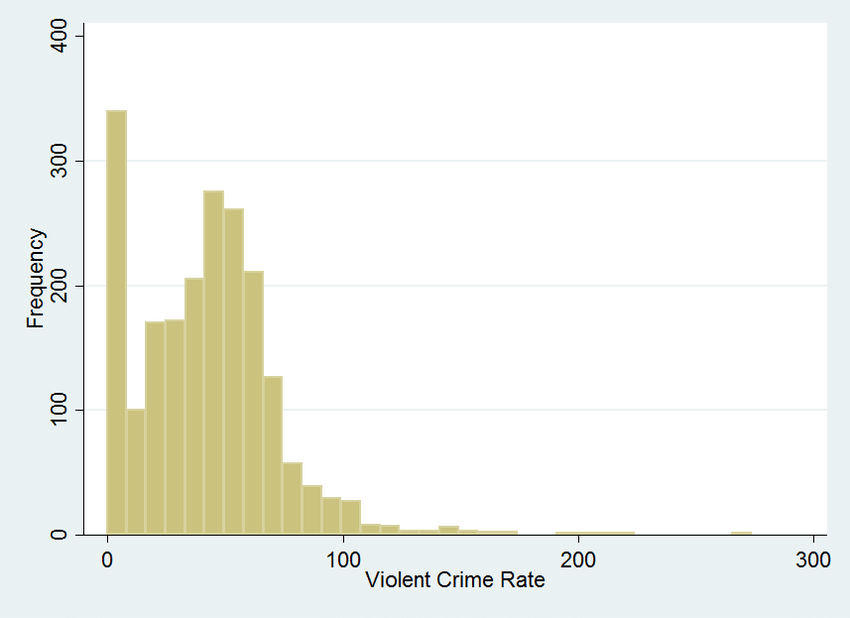
Histogram
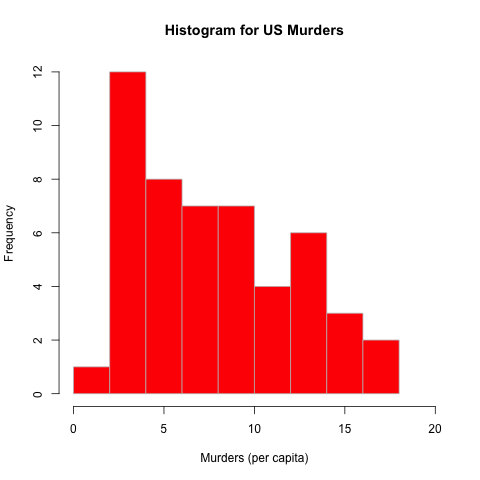
Histogram
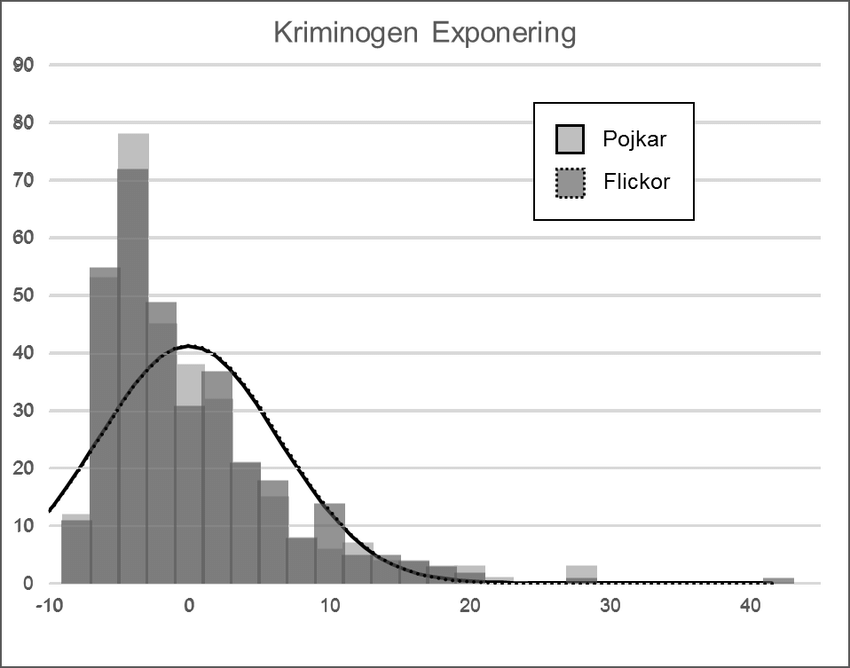
Linjediagram
Används främst för numeriska variabler.
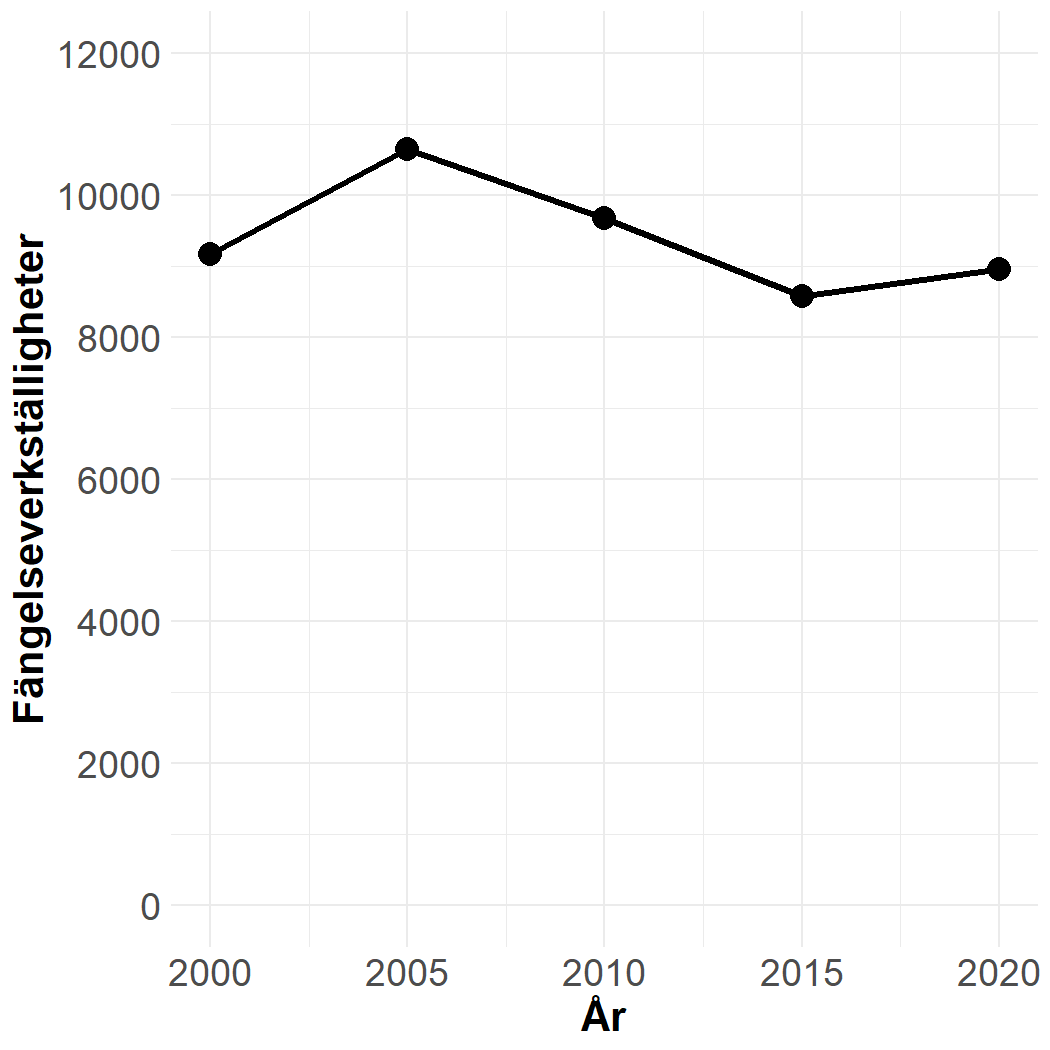
Linjediagram
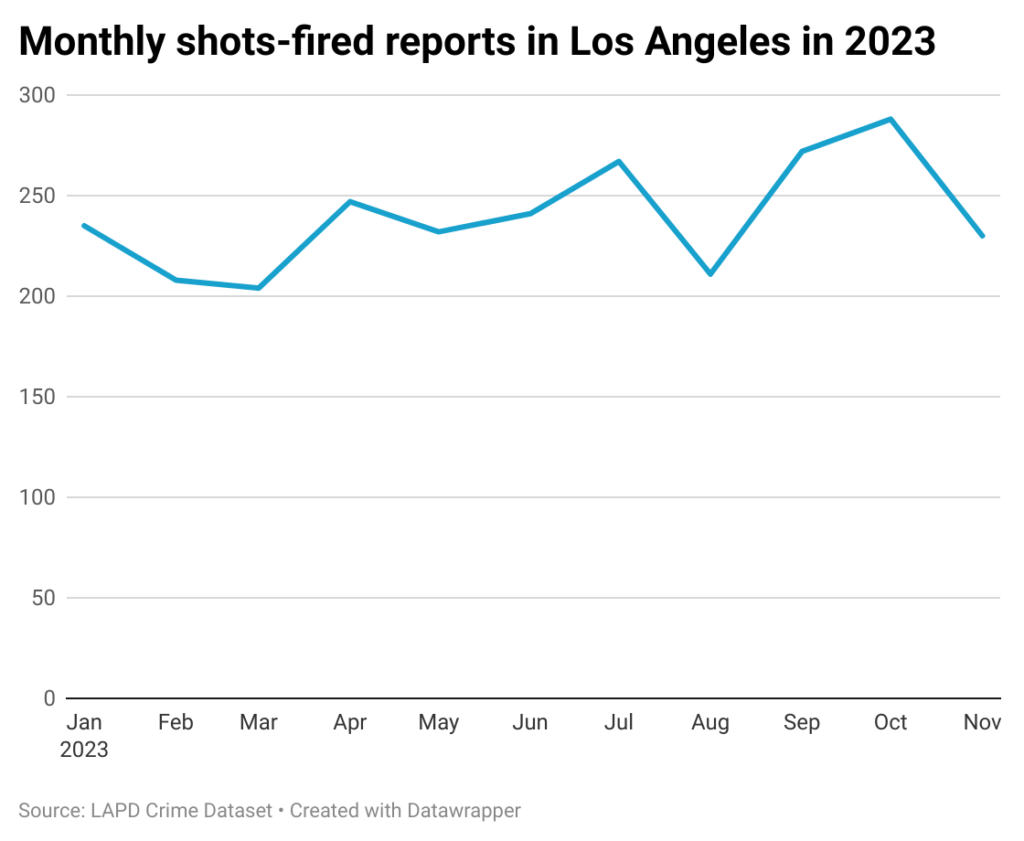
Linjediagram
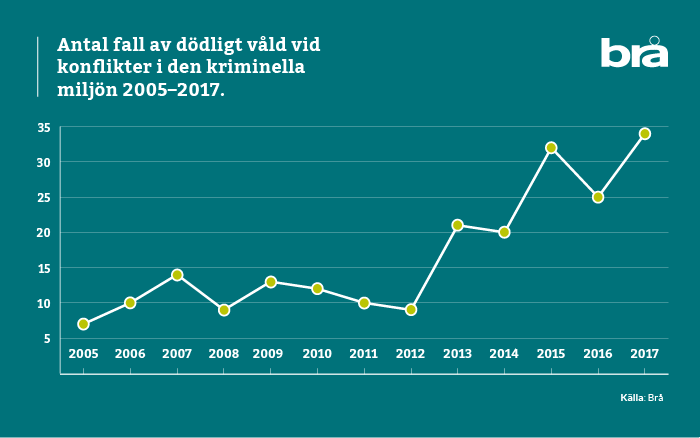
Linjediagram
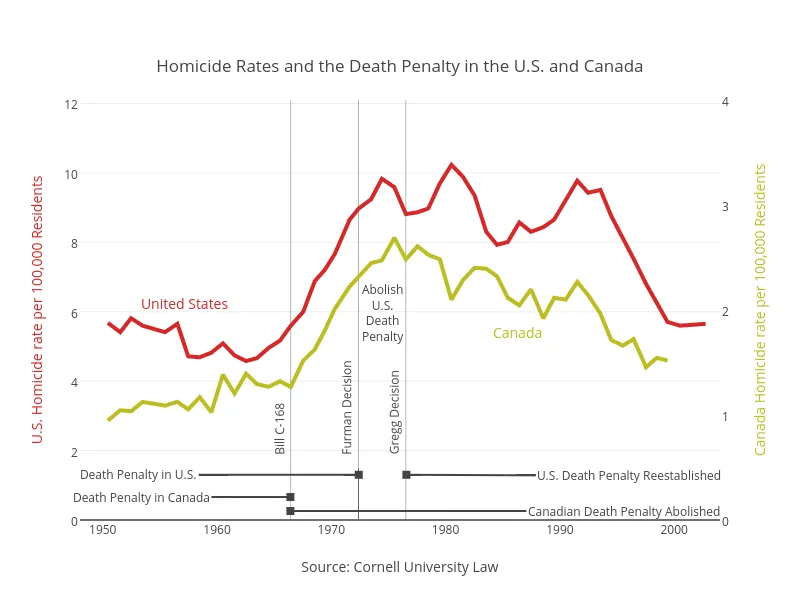
Linjediagram
Sammanfattning
Kvantitativa forskningsprocessen - Från hypotes till resultatpresentation
Datanivåer och variabeltyper - Nominal, Ordinal, Intervall, Kvot
Univariat beskrivande statistik - Frekvenser och andelar samt centralmått
Grafisk resultatpresentation - Olika typer av figurer beroende på datanivå